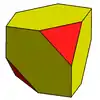
倒角四面體
在幾何學中,倒角四面體(英語:),又稱為交错截角立方体(英語:)是一種凸多面體,透過交替地將立方體截去頂點或在將四面體進行倒角操作——用六邊形取代其6邊。
 | |
| 類別 | 戈德堡多面體 |
|---|---|
| 對偶多面體 | 交錯三角化八面體 |
| 數學表示法 | |
| 康威表示法 | cT |
| 戈德堡符號 | GIII(2,0) |
| 性質 | |
| 面 | 4 正三角形 6 六邊形 |
| 邊 | 24 (2組) |
| 頂點 | 16 (2組) |
| 歐拉特徵數 | F=10, E=24, V=16 (χ=2) |
| 組成與佈局 | |
| 頂點佈局 | (12) 3.6.6 (4) 6.6.6 |
| 對稱性 | |
| 對稱群 | Tetrahedral (Td) |
| 特性 | |
| convex、 equilateral-faced | |
倒角四面體是一種戈德堡多面體,其符號為GIII(2,0)
相關多面體
| 多面體 | 平面鑲嵌 | 雙曲鑲嵌 | |||
|---|---|---|---|---|---|
| [3,3] | [4,3] | [5,3] | [6,3] | [7,3] | [8,3] |
 正方體 |
 菱形十二面體 |
 菱形三十面體 |
 菱形鑲嵌 |
 |
 |
 倒角四面體 |
 倒角正方體 |
 倒角十二面體 |
 正六邊形鑲嵌 |
||
| 類別 | 柏拉圖立體 | 卡塔蘭立體 | |||||
|---|---|---|---|---|---|---|---|
| 種子 |  {3,3} |
 {4,3} |
 {3,4} |
 {5,3} |
 {3,5} |
 aC |
 aD |
| 倒角 |  cT |
 cC |
 cO |
 cD |
 cI |
 caC |
 caD |
參見
參考文獻
- Antoine Deza, Michel Deza, Viatcheslav Grishukhin, Fullerenes and coordination polyhedra versus half-cube embeddings, 1998 PDF (页面存档备份,存于) (p. 72 Fig. 26. Chamfered tetrahedron)
- Chamfered Tetrahedron (页面存档备份,存于)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.