雙曲正弦
在數學中,雙曲正弦是一種雙曲函數,是雙曲幾何中,與歐幾里得幾何的正弦函數相對應的函數。雙曲正弦可以視為正弦函數的類似物,然而雙曲正弦不具備週期性,且在定義域為實數的情況下,其值域也包括了整個實數域。一般的正弦可以表示為單位圓上特定角構成之弦長的一半,或該角與圓之交點的y座標;而雙曲正弦則代表單位雙曲線上特定雙曲角構成之雙曲弦長的一半,或該雙曲角與單位雙曲線之交點的y座標。雙曲正弦一般以sinh表示[1],在部分較舊的文獻中有時會以表示。[2]
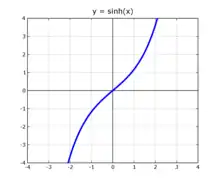 | |
| 性質 | |
| 奇偶性 | 奇 |
| 定義域 | (-∞,∞) |
| 到達域 | (-∞,∞) |
| 特定值 | |
| 當x=0 | 0 |
| 當x=+∞ | +∞ |
| 當x=-∞ | -∞ |
| 最大值 | +∞ |
| 最小值 | -∞ |
| 其他性質 | |
| 渐近线 | N/A |
| 根 | 0 |
| 臨界點 | N/A |
| 拐點 | 0 |
定義
雙曲正弦一般計為[3](有時會簡寫為[4]),其在複變分析中定義為:[5]
其中是複變指數函數。
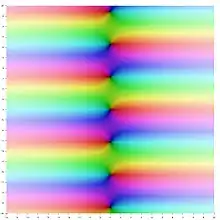
複數域雙曲正弦的色相環複變函數圖形
也就是說,雙曲正弦等同於指數函數與其倒數之差的一半[6]。雙曲正弦也可以視為自然指數函數的奇函數部分[7]
在雙曲幾何中,雙曲正弦函數類似於歐幾里得幾何中的正弦函數。[8]
性質
一般性質
參見
參考文獻
- (1999) Collins Concise Dictionary, 4th edition, HarperCollins, Glasgow, ISBN 0 00 472257 4, p. 1386
- Dr. Franz Brzoska, Walter Bartsch, Mathematische Formelsammlung. 2. verbesserte, Fachbuchverlag Leipzig. 1956 (德文)
- . International Organization for Standardization. [1 July 2010]. (原始内容存档于2014-03-26).
- Gradshteyn, Izrail Solomonovich; Ryzhik, Iosif Moiseevich. 6. Academic Press, Inc. 2000. ISBN 978-0-12-294757-5.
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- . mathworks. [2021-07-11]. (原始内容存档于2021-07-12).
- Richard Hensh. (PDF). math.msu.edu. [2021-07-11]. (原始内容存档 (PDF)于2021-07-11).
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. [2020-08-29] (英语).
- (PDF). mathcentre.ac.uk. [2021-07-11]. (原始内容存档 (PDF)于2021-01-19).
- (PDF). teaching.martahidegkuti.com. [2021-09-15]. (原始内容存档 (PDF)于2020-01-13).
- . www.mathsisfun.com. [2020-08-29]. (原始内容存档于2022-03-03).
- Osborn, G. . The Mathematical Gazette. July 1902, 2 (34): 189 [2021-09-15]. JSTOR 3602492. doi:10.2307/3602492. (原始内容存档于2021-11-01).
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.