初等函数

初等函数（基本函數）是由常函数、幂函数、指数函数、对数函数、三角函数和反三角函数等经过有限次的有理运算（加、减、乘、除、乘方、开方）及有限次函数复合所产生、并且在定义域上能用一个方程式表示的函数。 [1]

一般来说，分段函数不是初等函数，因为在这些分段函数的定义域上不能用一个解析式表示。

初等函数的全体对算术运算、复合和微分（求导）是封闭的，但对求极限、无穷级数以及积分不封闭。只有刘维尔函数（初等函数及其积分）的全体对积分才是封闭的。

此外，部分初等函数不是整函数，或者在复数域上是多值函数。

名称来源

之所以称这些函数为“初等函数”或“基本函数”（法语：fonction élémentaire），需要从微分代数的角度考虑。尽管“初等函数”这个概念最初是由约瑟夫·刘维尔引入的，但目前的通行定义是由约瑟夫·里特给出的：

一个微分域 $F$ ，定义为某一个域 $F_{0}$ 再加上一个函数对函数的映射 $u\rightarrow f(u)$ 。其中， $f(u)$ 满足以下条件：

f(u+v)=f(u)+f(v)

f(uv)=uf(v)+vf(u)

且该域内的任意常数 $C$ 都满足 $f(C)=0$ 。

在以上定义满足时，一个函数 $u$ 被称为 $F$ 上的初等函数，当且仅当该函数至少满足以下三者之一：

是 $F$ 上的代数函数；
是 $F$ 上的指数性函数，意即 $f(u)=uf(a),a\in F$ ；
是 $F$ 上的对数性函数，意即 $f(u)={\frac {f(a)}{a}},a\in F$ 。

常函数

称 $f(x)=C$ 为常数函数，其中C为常数，它的定义域为 $(-\infty ,\infty )$ 。
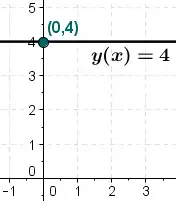
$常函数 f ( x ) = 4 {\displaystyle f(x)=4} 图像$

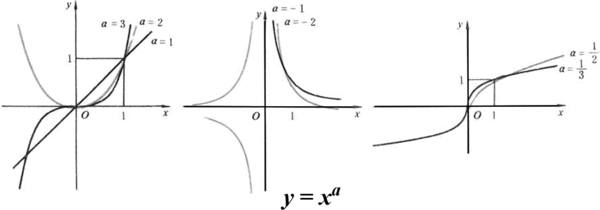
幂函数

称形如 $f(x)=Cx^{r}$ 的函数为幂函数，其中C, r为常数。幂函数的定义域与r的值有关，但是不管r取何值，该函数在 $(0,+\infty )$ 上总有意义。
几种常见的幂函数图像

指数函数

称形如 $f(x)=a^{x}$ 的函数为指数函数，其中a是常数， $a>0$ 且 $a\neq 1$ 。该函数的定义域为 $(-\infty ,+\infty )$ ，值域为 $(0,+\infty )$
$指数函数 y = e x {\displaystyle y=e^{x}} 的图像$

对数函数

称形如 $y=\log _{a}x\!$ 的函数为对数函数，其中 $a>0$ 且 $a\neq 1$ ，是指数函数 $y=a^{x}$ 的反函数。该函数定义域为 $(0,+\infty )$ ，值域为 $(-\infty ,+\infty )$
e, 绿色函数底数是2，而藍色函数底数是1/2。在数轴上每个刻度是半个单位。所有底数的对数函数都通过点(1,0)，因为任何数的0次幂都是1，而底数 β 的函数通过点(β ,1)，因为任何数的1次幂都是自身1。曲线接近 y 轴但永不触及它，因为x=0的奇异性。

三角函数

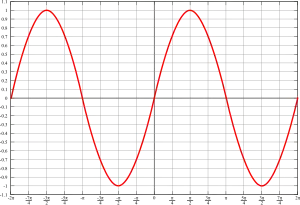
正弦函数

称形如 $f(x)=\sin x$ 的函数为正弦函数，它的定义域为 $(-\infty ,+\infty )$ ，值域为 $[-1,1]$ ，最小正周期为 $2\pi$ 。
正弦函数图像

余弦函数

称形如 $f(x)=\cos x$ 的函数为余弦函数，它的定义域为 $(-\infty ,+\infty )$ ，值域为 $[-1,1]$ ，最小正周期为 $2\pi$ 。
余弦函数图像

正切函数

称形如 $f(x)=\tan x$ 的函数为正切函数，它的定义域为 $\{x|x\neq k\pi +{\frac {\pi }{2}},\,k\in \mathbb {Z} \}$ ，值域为 $(-\infty ,+\infty )$ ，最小正周期为 $\pi$ 。
正切函数图像

余切函数

称形如 $f(x)=\cot x$ 的函数为余切函数，它的定义域为 $\{x|x\neq k\pi ,\,k\in \mathbb {Z} \}$ ，值域为 $(-\infty ,+\infty )$ ，最小正周期为 $\pi$ 。
余切函数]图像

正割函数

称形如 $f(x)=\sec x$ 的函数为正割函数，它的定义域为 $\{x|x\neq k\pi +{\frac {\pi }{2}},\,k\in \mathbb {Z} \}$ ，值域为 $(-\infty ,-1]\cup [1,+\infty )$ ，最小正周期为 $2\pi$ 。
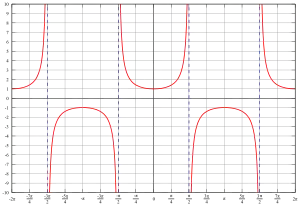
正割函数图像

余割函数

称形如 $f(x)=\csc x$ 的函数为余割函数，它的定义域为 $\{x|x\neq k\pi ,\,k\in \mathbb {Z} \}$ ，值域为 $(-\infty ,-1]\cup [1,+\infty )$ ，最小正周期为 $2\pi$ 。
余割函数图像

反三角函数

其它常见初等函数

双曲函数

双曲正弦函数： $y=\sinh x={\frac {e^{x}-e^{-x}}{2}}$
双曲余弦函数： $y=\cosh x={\frac {e^{x}+e^{-x}}{2}}$
双曲正切函数： $y=\tanh x={\frac {\sinh x}{\cosh x}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}$

反双曲函数

反双曲正弦函数： $y=\operatorname {arsinh} \,x=\ln(x+{\sqrt {x^{2}+1}})$
反双曲余弦函数： $y=\operatorname {arcosh} \,x=\ln(x+{\sqrt {x^{2}-1}})$

扩展阅读

Davenport, J. H.: What Might "Understand a Function" Mean. In: Kauers, M.; Kerber, M., Miner, R.; Windsteiger, W.: Towards Mechanized Mathematical Assistants. Springer, Berlin/Heidelberg 2007, p. 55-65. （页面存档备份，存于）

外部链接

Elementary functions at Encyclopaedia of Mathematics（页面存档备份，存于）
埃里克·韦斯坦因. . MathWorld.

伍胜健. . 北京大学出版社. 2009: 24. ISBN 9787301156858.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] 伍胜健. . 北京大学出版社. 2009: 24. ISBN 9787301156858.